VQ

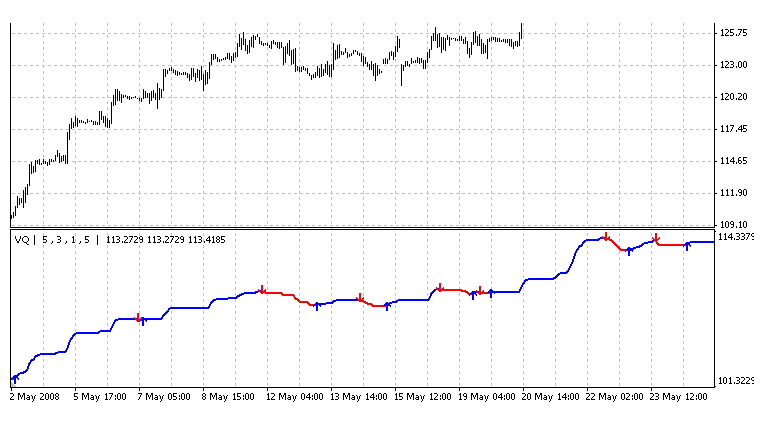
ここでは、VQがどのように算出されるのかをインジケーターVQのコードから読み解いていきます。インジケーターVQについて知らない方は、過去記事【VQとVQ_EA】をご覧ください。

過去記事【VQとVQ_EA】へ

VQの計算式

現在変動中のローソク足におけるVQの値は、次の計算式で割り出します。

MH = iMA(NULL, 0, Length, 0, Method, PRICE_HIGH, 0);
ML = iMA(NULL, 0, Length, 0, Method, PRICE_LOW, 0);
MO = iMA(NULL, 0, Length, 0, Method, PRICE_OPEN, 0);
MC = iMA(NULL, 0, Length, 0, Method, PRICE_CLOSE, 0);
MCS = iMA(NULL, 0, Length, 0, Method, PRICE_CLOSE, Smoothing);

VQ0 = MathAbs(((MC - MCS) / MathMax(MH - ML,MathMax(MH - MCS,MCS - ML)) + (MC - MO) / (MH - ML)) * 0.5) * ((MC - MCS + (MC - MO)) * 0.5);
SumVQ = Close[1] + VQ0;
if (Filter > 0 && MathAbs(VQ0) < Filter * Point) SumVQ = (前の足のSumVQ);

このSumVQが、VQの値です。

各変数の中身

上記コードからVQのパラメーターは次の役割があることが分かります。

Length 移動平均の期間
Method 平均方法
Smoothing 変数MCSのシフト数
Filter VQ値変動の最小値(単位: Point)

また、上記コード内の各変数は次のようになっています。

MH 高値の移動平均
ML 安値の移動平均
MO 始値の移動平均
MC 終値の移動平均
MCS Smoothing前の終値の移動平均

まずVQ0を算出

VQ0 =
MathAbs
(
   (
      (MC - MCS) / MathMax(MH - ML, MathMax(MH - MCS, MCS - ML))
      + (MC - MO) / (MH - ML)
   )
   * 0.5
)
* ((MC - MCS + MC - MO) * 0.5);
にゃんたにゃんた

あ～ややこしや～

ここで出てくるMathAbs()関数は()括弧内の絶対値、MathMax()関数は()括弧内の２つの値の大きい方を求める関数です。

ごちゃごちゃしてるので、紙に書いて確認すると良いです^^;

(MH – ML), (MH – MCS), (MCS – ML) のうち最大のもので(MC – MCS) を割ったものと、
(MH – ML) で (MC – MO)を割ったものを足して0.5をかけたものと、
(MC – MCS + MC – MO) に0.5をかけたものをかけた値がVQ0となるでしょうか^^;

変動幅フィルター

VQの値となる変数SumVQは、前回終値Close[1]にVQ0を足すのですが、Filterポイント未満のVQ値変動は変動無しとして補正しています。

SumVQ = Close[1] + VQ0;
if (Filter > 0 && MathAbs(VQ0) < Filter * Point) SumVQ = (前の足のSumVQ);

シグナル(アロー)発生条件

今までと反対方向への変化があった場合にシグナル（矢印）を表示させて、売り買い交互のシグナルになるようにしています。

次回記事【VQをEA内で計算する方法】へ